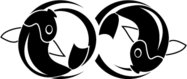Personalization

Anatomical Modeling

Current tomographic imaging modalities allow the geometrically accurate reconstruction of an individual's cardiac anatomy. A key objective is the conception of methods which allow to turn such tomographic image stacks into discrete anatomical representations which can be used for modeling cardiac physiology.

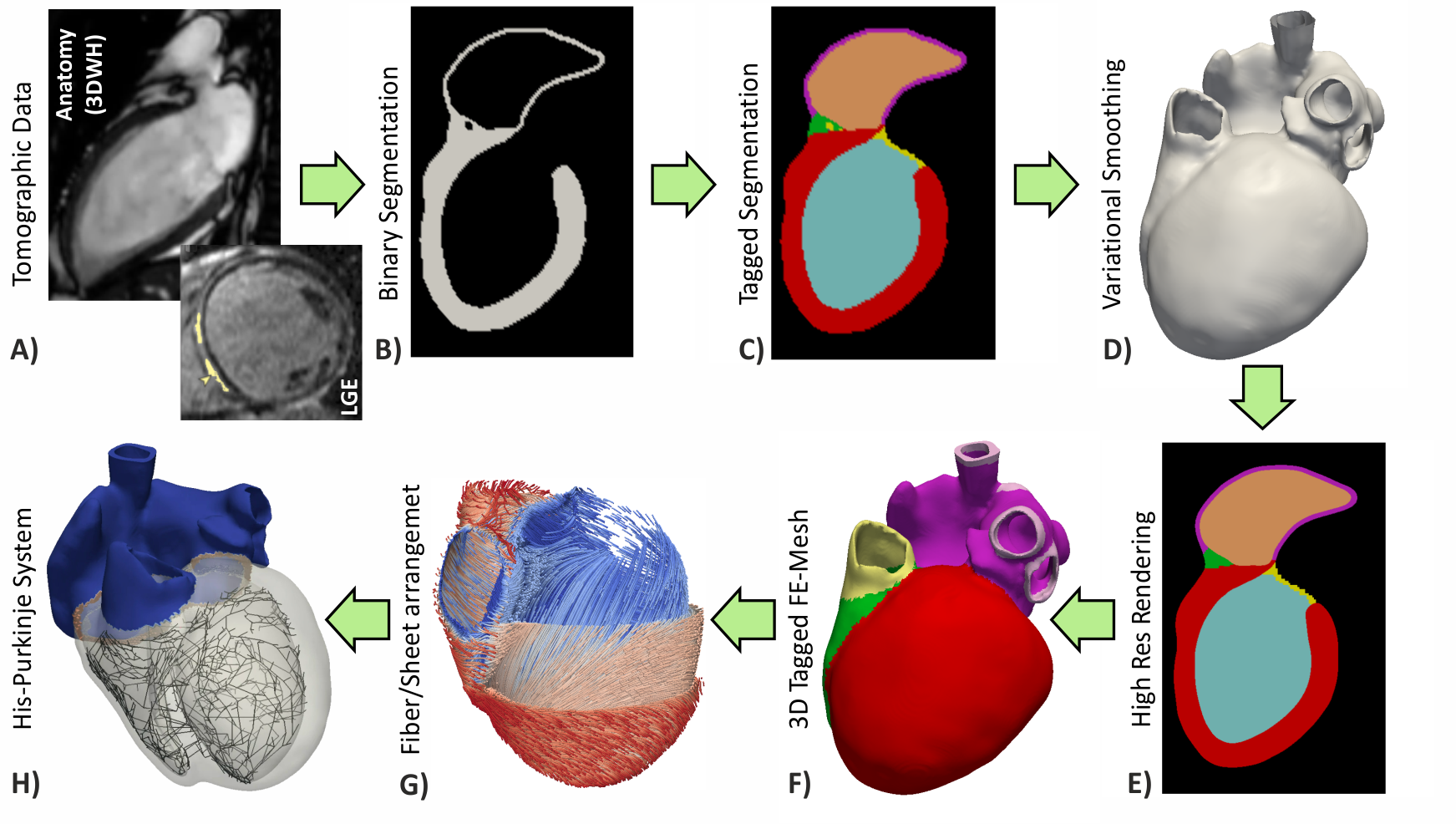
Figure: Workflow for the generation of cardiac models from medical image data
Tagged, high resolution models of the cardiac anatomy are generated as follows: A) Tomographic image datasets obtained with various MRI or CT scans B) are segmented to delineate cardiac anatomy from background and C) later sub-classified to generate label field. D) Surfaces of the segmentation are extracted and smoothed by a variational method to remove jagged boundary artefacts due to limited image resolution. E) The smoothed surface is re-rasterized at a high resolution and label field are mapped to the new image stack. F) The high resolution image stack is finally fed into an image-based mesh generator to construct a high resolution, labeled, 3D anatomical model which closely matches the source segmentation. G) Information on tissue orthotropy due to the arrangement of fibers and sheets is generated using a rule-based method using anatomical information as implemented, for instance, in the Laplace-Dirichlet Rule-based Algorithm. H) A topologically realistic representation of the His-Purkinje system is mapped onto the model using an automated method based on Universal Ventricular Coordinates.

Image Based Mesh Generation

The conversion of tomographic imaging data into discrete finite element models relies upon model generation pipelines as illustrated in the figure above. The desire to translate the image data into finite element space and tailor it to specific physics may impose strikingly different requirements. Electrophysiology models feature fast transients in time and steep wave fronts in space, which makes high spatio-temporal resolutions necessary to capture these dynamics. In contrast, due to the smoother spatio-temporal characteristics of mechanical deformation, numerical constraints upon discretization are less severe. Preferably, relevant anatomical details and a sufficiently smooth surface of organs need to be preserved. Moreover, anatomical classification of voxel groups (e.g. torso, lung, heart, ...), obtained during the segmentation process, need to be transferred. These requirements can be met using an image-based unstructured mesh generation technique which produces conformal, boundary-fitted, hexahedra-dominant and adaptive meshes in a fully automatic fashion.

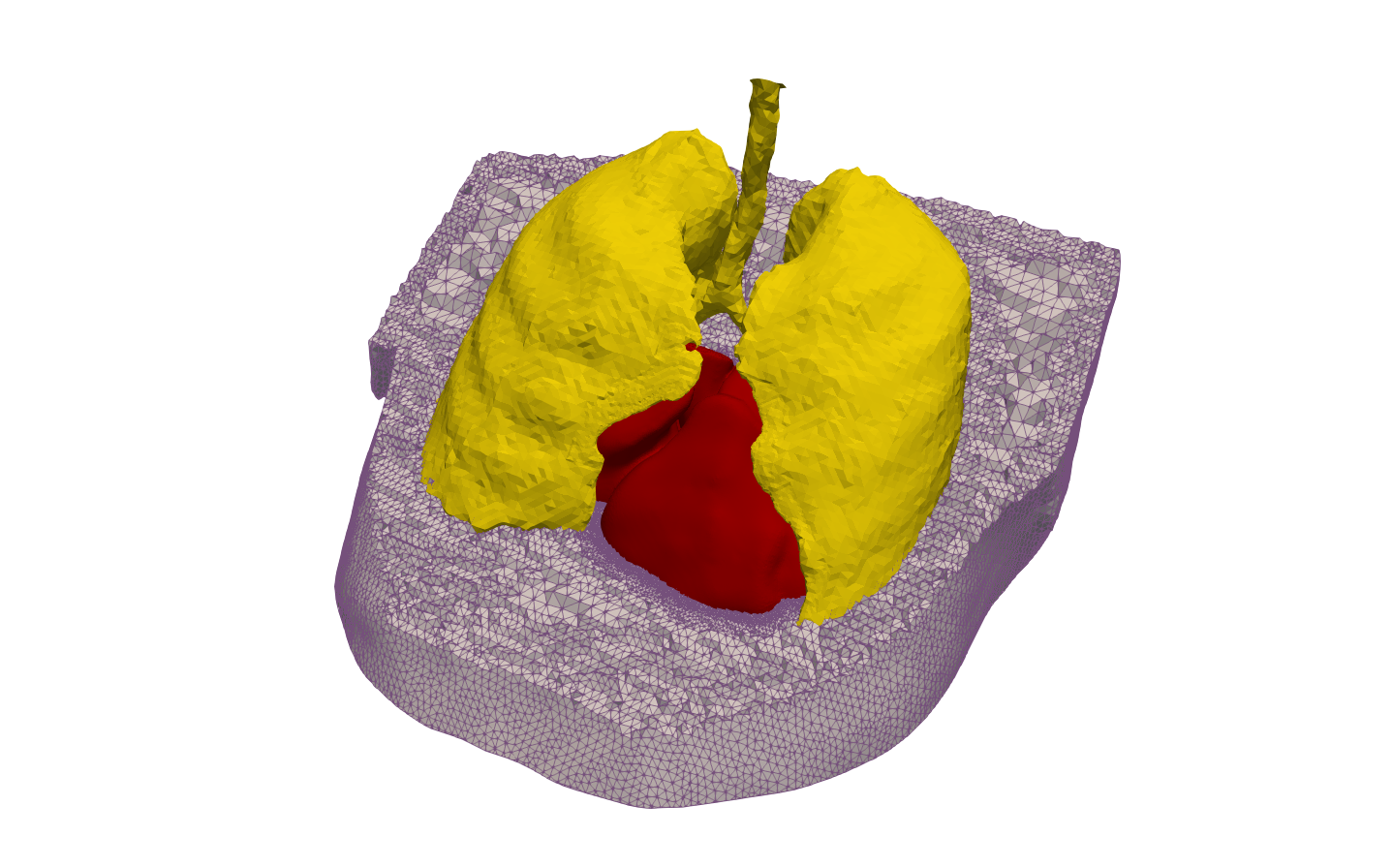
Figure: Torso model
Slice of torso model including lungs and four-chamber heart tesselated with tetrahedral elements. Wireframe view highlights increasing mesh resolution towards the heart.

Rule-Based Fiber Algorithm

Geometric models derived from imaging data do not include information on the distribution of fiber orientations. Knowledge of the structural anisotropy, however, is essential for modelling the electrical conduction and active force generation. In absence of histology or ex-vivo diffusion tensor MRI, mathematical rules are applied to grade up personalized anatomical models.

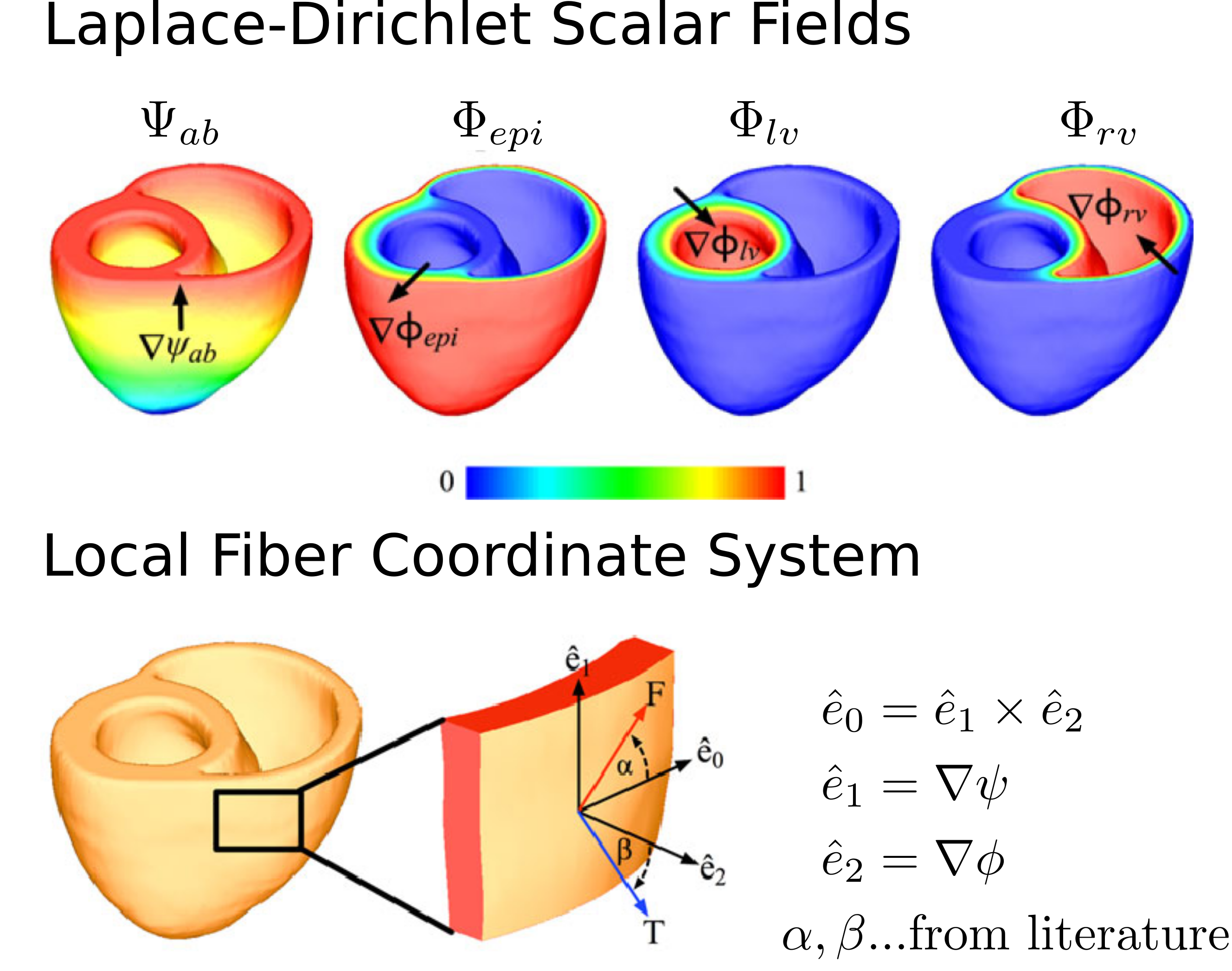
Figure: Laplace-Dirichlet Scalar Fields
Computed Laplace solutions with arrows showing in the direction of the gradient of the Laplace-Dirichlet scalar field. Local Fiber Coordinate System: Circumferential e0, apico-basal e1, and transmural e2 axes are derived from the Laplace solutions. With the help of the user provided input angles α and β, the rotation of fiber direction F and the rotation of sheet direction T are set up. [Bayer, Annals of Biomedical Engineering, 2012]

Universal Ventricular Coordinates (UVC)

Performing studies with anatomically accurate models of patients has become the state-of-the-art in computational modeling in cardiac electro-mechanics. Their application in a clinical context, enriched with patient-specific functionalization for diagnostics and therapy planning, shows high promise. Tuning spacial and temporal parameters involves labor and time-intensive workflows with the need of efficient and easily applicable data structures. For this sake UVC coordinates were introduced to quickly navigate within a ventricular geometry or map data between comparable geometries.

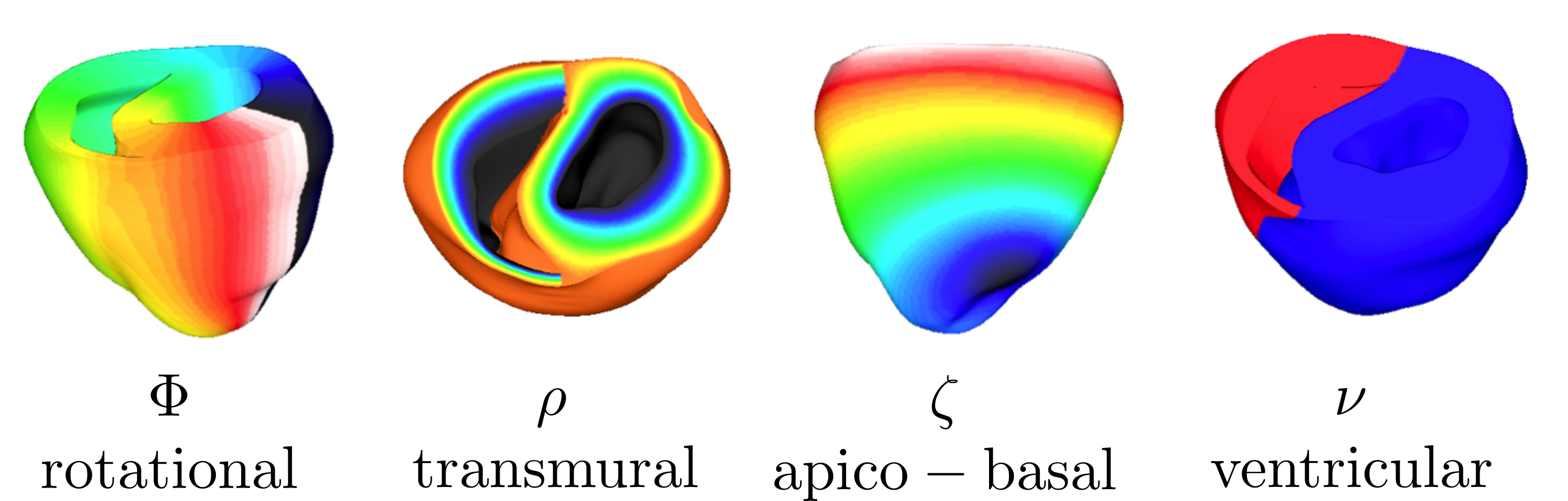
Figure: UVC coordinates
The UVC coordinates comprise four unique coordinates. The rotational coordinate Φ represents the circumferential rotation around the long axes of LV and RV. The transmural coordinate ρ represents the distance from the epicardium to the endocardium. The shortest geodesic distance from the apex to the base accounts for the apico-basal coordinate ζ. The transventricular coordinate ν determines whether the other three coordinates are within the LV or RV of the biventricular mesh. [Bayer, Medical Image Analysis, 2018]

Digital Twinning

A digital twin is a digital replica of an individual person.

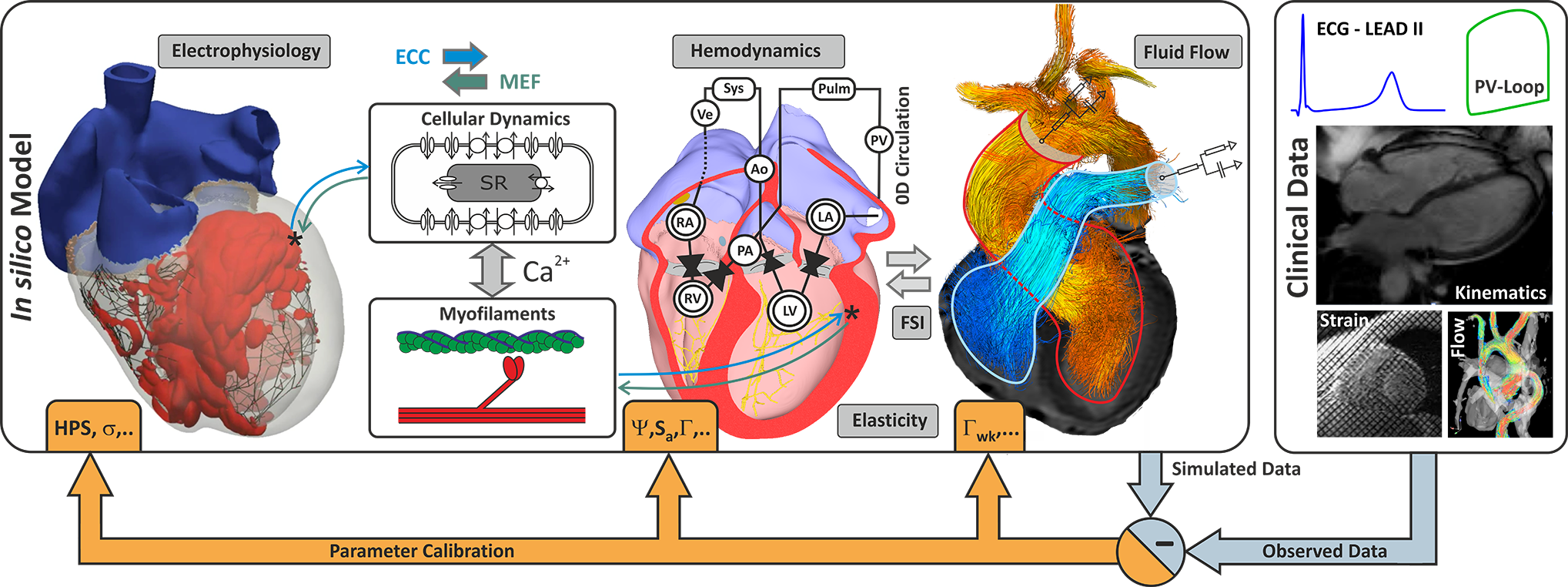
Figure: Personalization of model parameters.
Generation of patient-specific anatomical models of the heart from image data. The model simulates the interaction of electric wave propagation, chemical processes, and muscle contraction, leading to heart deformation and blood circulation. By calibrating with clinical data, we create a digital twin of a specific patient. This model allows for parameter adjustments to develop synthetic twins, enhancing the dataset with variations in tissue properties and circulatory conditions, including diseased valves.
Video 1: Extracellular potentials in heart and torso
Electrical sources generated in the mycoardium during activation and repolarization sequence are linked to an extracellular potential field throughout heart and extracadiac domains.

Mechanical Personalization

The detailed workflow used for parameterization of electro-mechanical LV models is described in [Augustin et al.,2016] , personalizing passive and active mechanical model components as well as circulatory components. Constitutive relations accounting for the passive mechanical properties of the cardiac tissue are represented in terms of the Guccione Model . From the anatomical models at end-diastolic state, a stress-free reference configuration is computed using default material parameters and end-diastolic pressure in the LV. This is accomplished by unloading the geometry using a backward displacement method. The EDPVR is fitted to the empiric Klotz EDPVR using default values from literature for the parameters [Guccione et al.,1991] adapting only the stiffness parameter \(C_{\mathrm{Guc}}\). A simplified phenomenological contractile model was used to represent active stress generation , which was fitted using default values of \(\tau_\mathrm{C}\), \(\hat{S}_{\rm a}\), \(\tau_\mathrm{R}\) as initial guess. \(T_\mathrm{dur}\) was initialised with the RT interval observed in the ECG. A linear mapping was used to correct the active stress model parameters. When measured pressure traces \(p_\mathrm{lv,m}(t)\) were not available, only \(\hat{S}_{\rm a}\) was iteratively adjusted by a fixed-point iteration \(\hat{S}_{{\rm a},i+1} = \hat{S}_{{\rm a},i} \cdot \hat{p}_{\mathrm{lv}}/\hat{p}_{\mathrm{lv},i}\). Otherwise, rate of rise \(\tau_\mathrm{C}\) and decline \(\tau_\mathrm{R}\) of active stress were adjusted accordingly using \(\frac{p_{\rm lv,m}}{dt}|_\mathrm{max}\) and \(\frac{p_{\rm lv,m}}{dt}|_\mathrm{min}\) as references and fitted in an similar manner. Circulatory components in terms of the three-element Windkessel model were identified separately using a global-local optimization approach. Both workflows are visualized below.

Figure: Parameterization of mechanical (lower panel) and circulatory model components (upper panel)
The three-element Windkessel afterload parameters \(\{Z, Z_{\rm v}, R, C\}\) were identified using measured haemodynamic parameters. Subsequently, the electro-mechanical LV model is fitted. First, the biomechanical bulk modulus \(C_\mathrm{Guc}\) is adjusted to fit the passive behaviour of the LV model to the empirical approximation of the end-diastolic pressure volume relation (EDPVR) due to Klotz, using \(\{V_\mathrm{ed}, p_\mathrm{lv,ed}\}\) as inputs. Using the fitted afterload model coupled to the EM LV model through a resistive valve model, the active stress model is parameterised using fixed-point iterations to adjust the phenomenological active stress model parameters, \(\{\tau_\mathrm{C}, \hat{S}_{\rm a}, T_\mathrm{dur}, \tau_\mathrm{R}\}\), using the discrepancy between measured and simulated \(p-V\) metrics during isovolumetric contraction and ejection.