Simulations of any aspect of cardiac function at the organ scale, be it electrophysiology, deformation, hemodynamics or perfusion, is a computationally vastly expensive endeavor. Electrophysiological simulations alone are expensive due to the spatio-temporal characteristics of excitation spread in the heart. The upstroke of the action potential is fast, lasting less than 1 ms, which translates into a steep wave front in space of an extent of less than 1 mm. Thus rather fine spatio-temporal discretizations are necessary to solve the underlying bidomain equations with sufficient accuracy. Cauchy’s equation does not demand such a high spatio-temporal resolution as deformation takes places at slower rates over larger spatial scales, but the non-linearity of the problems renders its solution even more expensive. Moreover, virtually all scenarios considering the clinical application of in-silico models critically depend on the ability of personalizing models to provide complementary input for diagnosis [Niederer et al, 2010], disease stratification [Arevalo et al, 2016], therapy optimization, planning and outcome prediction in a patient-specific manner. Such applications require a substantial number of forward simulations as these are integrated in an optimization loop where often sizable parameters spaces must be explored to iteratively re-parameterize models until a sufficiently close match with clinical data is achieved.

The problem of executing simulations in a tractable manner within time scales compatible with academic research or even clinical work flows is addressed by devising efficient numerical methods and algorithms which must be implemented to efficiently exploit modern high performance computing hardware. Alternatively, smarter model formulations alleviating the need for punitively fine spatio-temporal resolution or model order reduction techniques are promising strategies for achieving a significant reduction in computational costs.

Massively parallel supercomputing

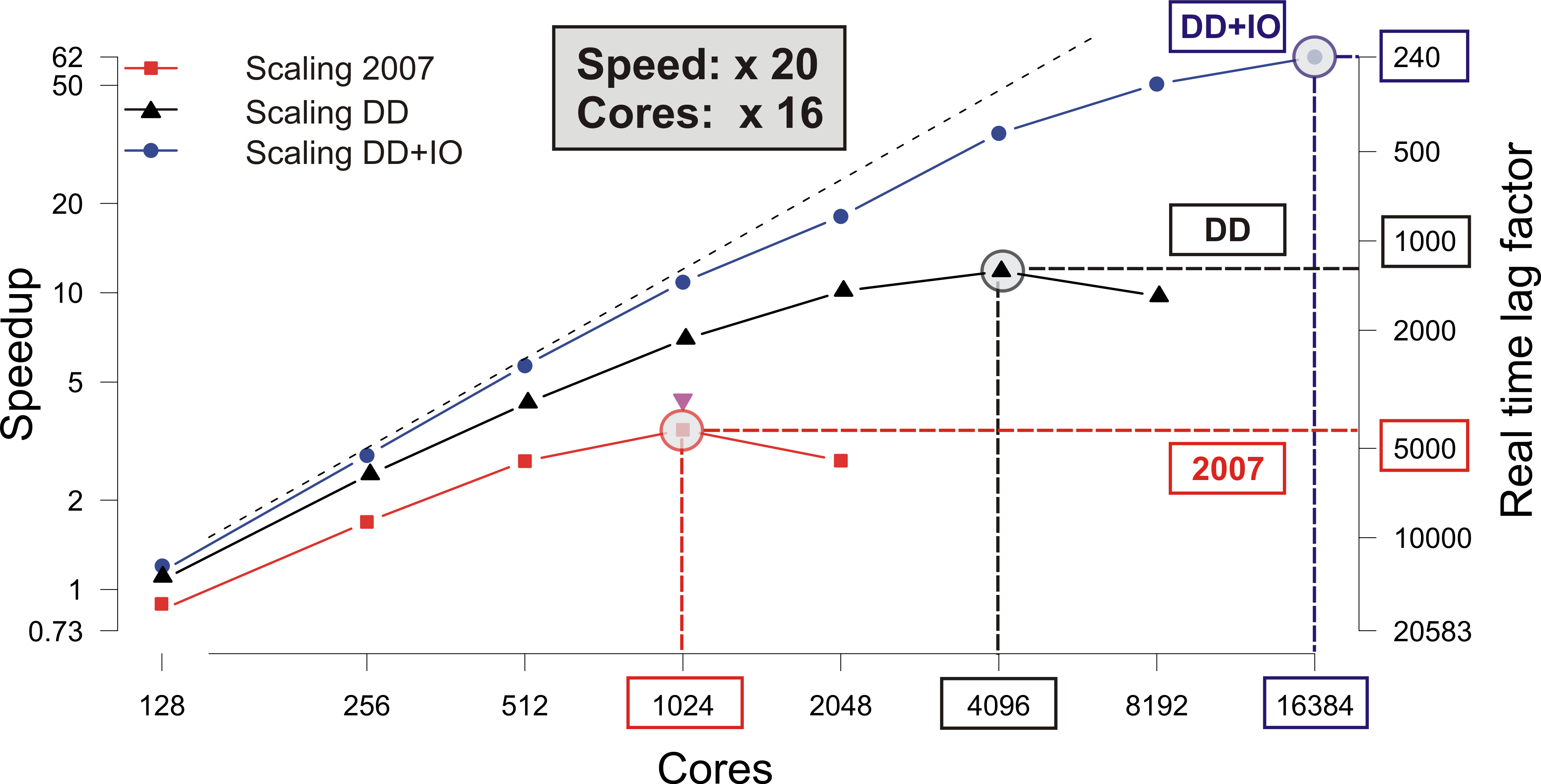
Increasing the number of compute cores to reduce execution times is referred to as strong scaling. Its effectiveness is limited by the ratio between local compute work (volume) to the cost of communication (surface). With an increasing number of cores the local compute load decreases, but the relative cost of communication increases, that is, the volume to surface ratio becomes increasingly smaller and starts limiting strong scalability. At a certain number of compute cores referred to as the limit of strong scalability no further gains can be achieved from adding more compute cores as the overall execution time will not be further reduced. Rather, communication costs start to dominate, leading to an increase in execution time despite the use of more compute cores. Further, with a very high number of compute cores engaged the cost of I/O increases as results must be collected from a large number of cores across a communication network. From a numerical point of view, for optimizing strong scaling behavior workload and communcation cost must be distributed evenly, communication must be minimized by decomposing the solution domain to obtain volumes with minimal surfaces, and the cost of I/O must be hidden.

Figure: Strong scalability

Improved domain decomposition (DD) to reduce communication costs combined with asynchronuous I/O techniques to hide the otherwise significant cost of I/O due to blocking of computations led to significantly more favorable strong scaling properties. Shown are improvements over an implementation using a naive grid partitioning based on linear decomposition based on nodal indices and a standard sequential blocking I/O implementation. Efficient strong scaling could be improved from 1024 cores up to 16k cores. For details see Niederer et al, Front. Physiol 2011.

Use of Accelerators