Formation & Maintenance of Arrhythmias

Arrhythmias are abnormal heart rhythms that occur due to disruptions in the electrical signals that regulate the heart's pumping action. These disruptions can arise from issues with how electrical impulses are generated or how they propagate through the heart's conduction system.

1. Abnormal Impulse Generation

• Enhanced Automaticity: Normally, the sinoatrial (SA) node controls the heart rate, but other areas of the heart can abnormally take over. This happens when non-pacemaker cells develop the ability to spontaneously depolarize, causing ectopic beats or tachycardia. Conditions like ischemia, electrolyte imbalances (e.g., potassium abnormalities), and certain drugs (e.g., digoxin) can enhance automaticity.
• Triggered Activity: Abnormal secondary depolarizations following the normal action potential can lead to arrhythmias. These are categorized as:
  • Early Afterdepolarizations (EADs): Occur during phases 2 or 3 of the cardiac action potential, usually caused by prolonged repolarization, leading to further electrical instability and the risk of arrhythmias.
  • Delayed Afterdepolarizations (DADs): Occur after full repolarization (phase 4), often due to intracellular calcium overload, which can be seen in conditions like heart failure or digitalis toxicity.

2. Abnormal Impulse Conduction

• Re-entry Circuits: Re-entry occurs when a normal electrical impulse gets caught in a loop of tissue that allows it to continuously re-excite the heart. This can happen in atrial fibrillation, ventricular tachycardia, or AV nodal reentrant tachycardia (AVNRT).
• Conduction Block: A delay or complete block in the transmission of electrical impulses through the heart, often due to fibrosis or damage to conduction pathways. This can result in bradycardia or contribute to re-entrant arrhythmias.

Pacing Therapy

Cardiac tissue can be depolarized to initiate wavefront propagation by applying electrical current through an electrode located adjacent to the tissue. Excitation may occur near the anode as well as near the cathode during both the onset (make) as well as the end (break) of the stimulus. These excitation processes are governed by four distinct mechanisms: cathode make (CM), anode make (AM), cathode break (CB) and anode break (AB) [Roth, 1995]. Except for CM excitation which can be explained with basic laws of electricity in 1D, multi-dimensional active bidomain models are necessary to gain insights in all other cases. An overview of the evolution of transmembrane voltages in the vicinity of a physical anode or cathode during and after delivery of a stimulus current is summarized below.

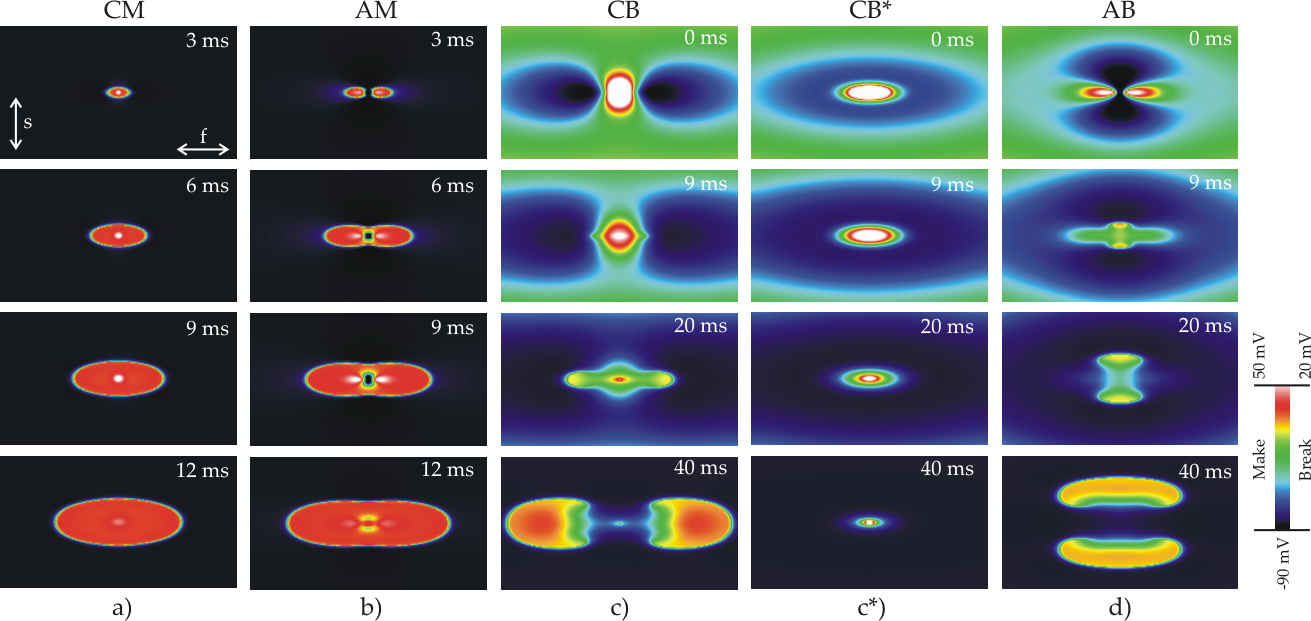
Figure: Overview of the evolution of transmembrane voltages in the vicinity of a physical anode or cathode during and after delivery of a stimulus current.

The heart can be electrically stimulated using current pulses in four distinct ways: (1) by initiating a pulse with negative amplitude (cathode make, CM), (2) by initiating a pulse with positive amplitude (anode make, AM), (3) by terminating a pulse with negative amplitude (cathode break, CB), and (4) by terminating a pulse with positive amplitude (anode break, AB).

Defibrillation Therapy

Cardiac defibrillation, as accomplished either externally or internally by automatic, implantable devices (ICDs), constitutes the most important means of combating sudden cardiac death. While ICD therapy has proved to be efficient and reliable, defibrillation is a traumatic experience due to the pain associated with shock delivery. Thus, research on defibrillation mechanisms, particularly aimed at lowering defibrillation voltage, remains an important topic. Advancing our understanding towards a full appreciation of the mechanisms by which a shock interacts with the heart is the most promising approach to achieve this goal.

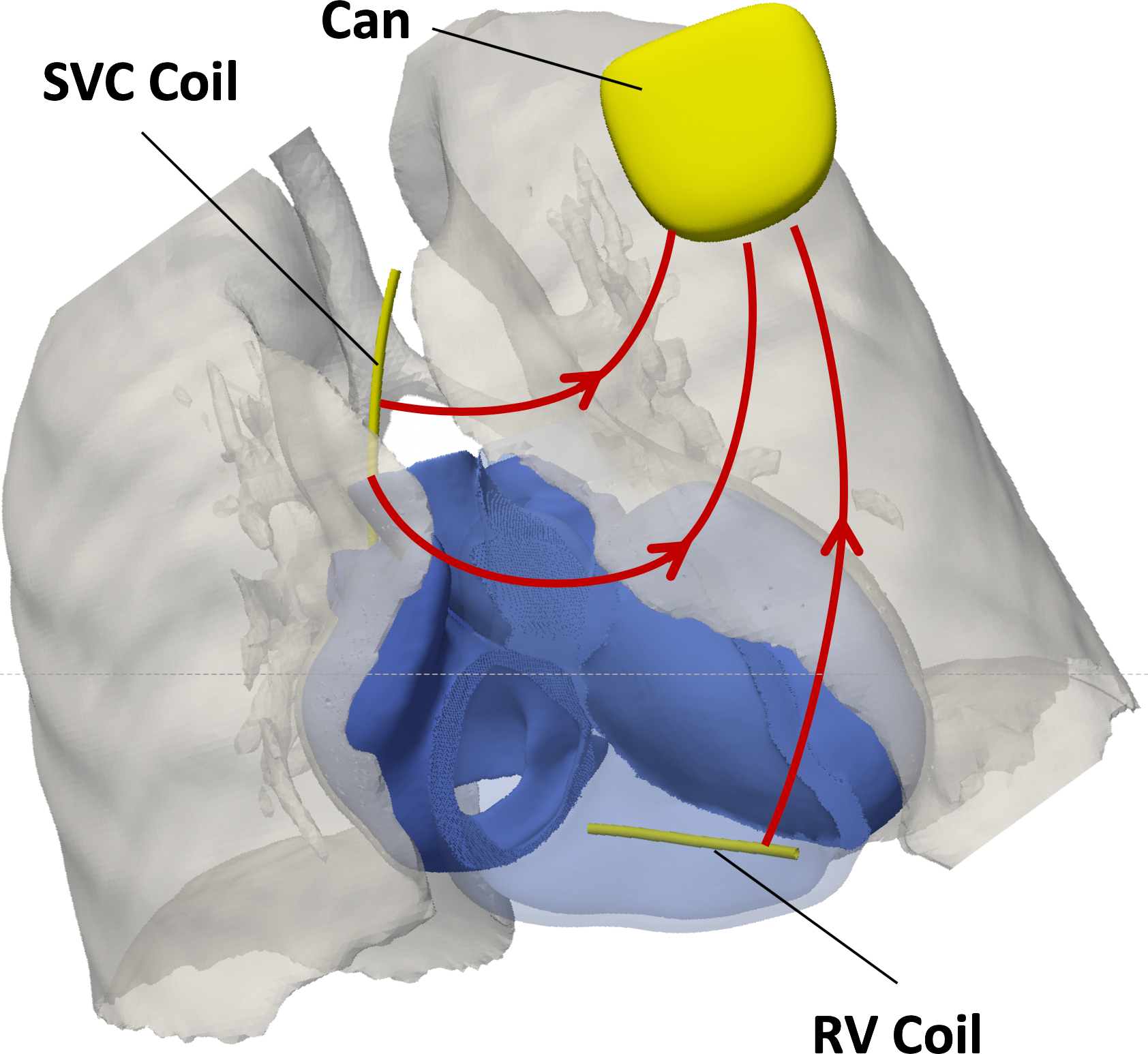
Internal defibrillation by ICD therapy is administered in two different forms, either with transvenous (TV-ICD) systems where electrode coils are inserted in the cardiac blood pool, or with leadless subcutaneous (S-ICD) systems where electrodes are implanted under the skin. The S-ICD system offers advantages, but owing to the wider range of feasible implant locations rationalization of an optimal lead placement is more challenging.

Reasons of success or failure of defibrillation shocks are multifactorial. Shape, size and location of electrodes as well as the timing (relative to an ongoing reentrant activation pattern), polarity, duration and waveform of the shock pulse play important roles. As ICD shocks are delivered by capacitive discharge, the exponential decay of waveforms is governed by the tissue's impedance governing the current flow between coils and can. The impact of the shock-induced electric field on the myocardium depends on on field strength \( \nabla \) and the spatial heterogeneity of the field as quantitatively by the activation function:

Activating Function

A theoretical concept termed activating function [Rattay, 1986], has proved to be useful for analyzing the etiology of VEPs. Rearranging the bidomain equation governing the intracellular potential \( \phi_{\rm i} \) yields $$ I_{ion}(s,v) + \frac{\partial v}{\partial t} - \nabla \cdot \left( \boldsymbol{\sigma_i}\nabla v \right) = \nabla \cdot \left( \boldsymbol{\sigma_i}\nabla u \right) $$ where the activating function, \( S \), in its most general form is the term on the right-hand side [Sobie, 1997]. When a stimulus is applied to tissue at rest, all terms on the left-hand side of the above equation are zero. The extracellularly applied stimulus establishes a potential field \( \phi_{\rm e} \) which drives the initial change in membrane voltage \( V_{\rm m} \). Expanding \( S \) $$ S = \nabla \cdot \left( \boldsymbol{\sigma_i}\nabla u \right) = \boldsymbol{\sigma_i} \colon \nabla \left(\nabla u \right) + \left( \nabla \cdot \boldsymbol{\sigma_i} \right) \cdot \nabla u $$ reveals that the sufficient conditions for \( S \) being non-zero are either spatial non-uniformity in applied electric field, or non-uniformity in tissue architecture.

The many factors involved, combined with the variability of reentrant activation patterns and structural/anatomical factors renders ICD therapy a complex optimization problem.